Loading...
Graphs of Linear Equations in Two Variables
A
B
C
. . . .

Slope of a Line

In the preceding example, it does not matter which of the two given points is assigned as ( x 1 ,   y 1 ) or ( x 2 ,   y 2 ). To illustrate this, let ( x 1 ,   y 1 )=(5,  6) and ( x 2 ,   y 2 )=(1,  3); that is, x 1 =5, y 1 =6, x 2 =1, and y 2 =3. Then the slope of the line is given by

m= y 2 − y 1 x 2 − x 1 = 3−6 1−5 = −3 −4 = 3 4 .

The figure below shows the line that passes through the points (5,  6) and (1,  3).

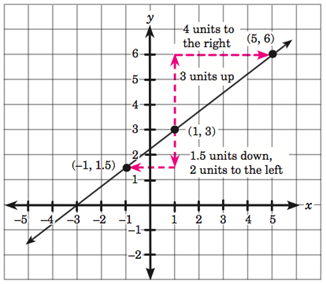
You learned that the slope (which, in this case, is 3 4 ) is the ratio of the rise to the run. This means that to go from one point to another on the line above, every vertical change of 3 units (which is the rise) corresponds to a horizontal change of 4 units (which is the run).

Notice that when a line rises from a left to right, it has a positive slope. The next example shows a line with a negative slope.