Conditions for Triangle Congruence
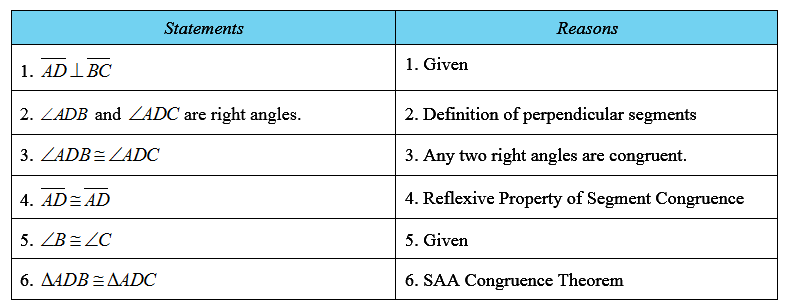
Example
In the given figure to the right,
is perpendicular to
and
Prove that

Solution
Proof:
Triangles ADB and ADC on the previous example are called adjacent triangles since they have a common side, which is
Bear in mind that triangles with two pairs of congruent sides and one pair of congruent nonincluded angles do not necessarily coincide, and hence, are not necessarily congruent. There is no SSA congruence. There is also no AAA congruence.
