Types of Statements
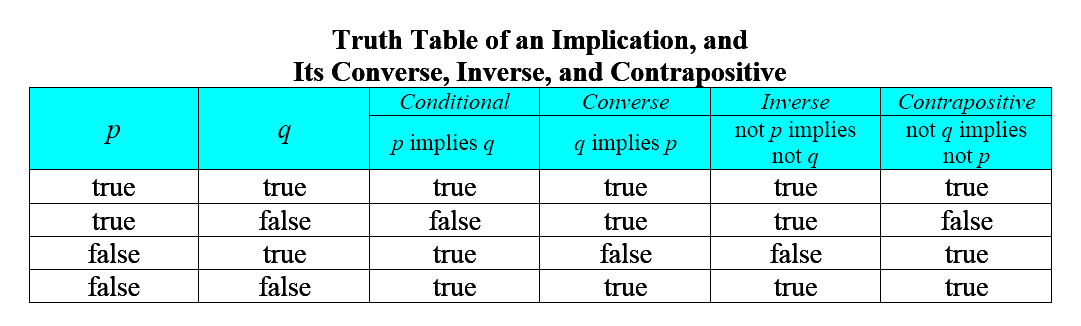
Three statements can be formed from an implication "If p, then q." These are its converse, inverse, and contrapositive.
Definition
Consider the statement "If p, then q."
- The converse of the given statement is "If q, then p."
- The inverse of the given statement is "If not p, then not q."
- The contrapositive of the given statement is "If not q, then not p."
Definition
Consider the statement "If p, then q."
- The converse of the given statement is "If q, then p."
- The inverse of the given statement is "If not p, then not q."
The following table summarizes the truth values of an implication, and its converse, inverse, and contrapositive: