Patterns and Inductive Reasoning (2)
An algebraic approach in finding the pattern in the previous page is to express the triangular numbers as the sum of each row of dots in the triangular pattern.
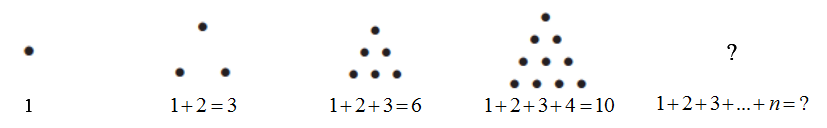
The number of handshakes is the sum of n consecutive numbers; that is,
You can derive the rule algebraically by adding 1 + 2 + 3 + ... + (n − 2) + (n − 1) + n to itself, and then dividing the sum by 2.
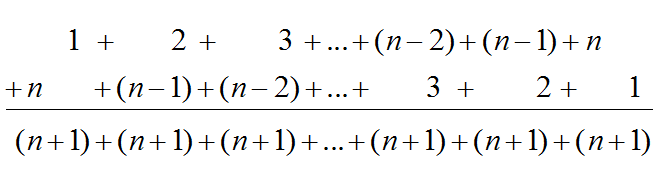
There are n terms of that sum up to If you divide this sum by 2, you will derive the Gaussian pattern,
The Gaussian pattern was named in honor of Carl Friedrich Gauss (1777–1855), a German mathematician. Mathematicians use inductive reasoning to find patterns and new rules or conjectures.
