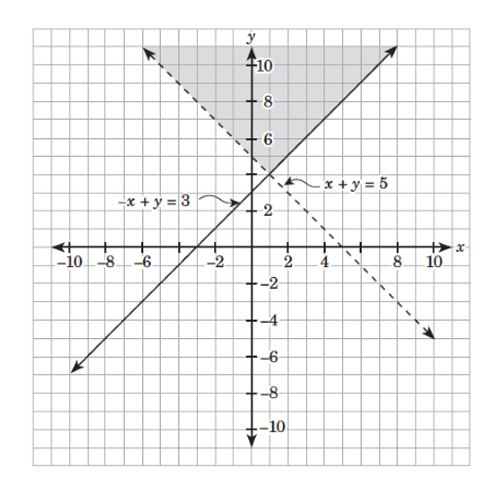
Graph the solution set of the following system of linear inequalities:

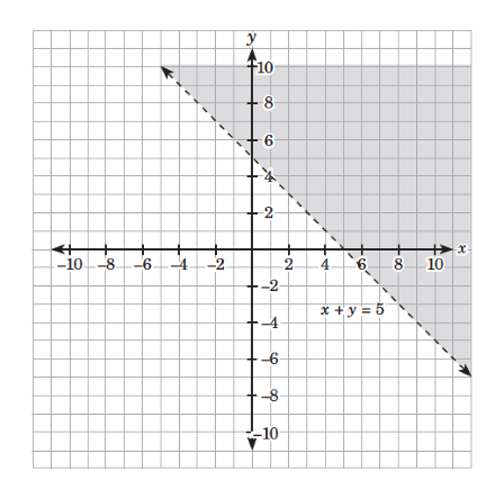
First, graph each linear inequality of the given system. The graph of $x+y\text{ > }5$ has a dashed boundary line with the equation $x+y=5.$

Using $(0,0)$ as the test point, you will get $0\text{ > }5,$ which is false. Hence, the graph of $x+y\text{ > }5$ is the region on the side of the boundary line not containing the point $(0,0).$ Refer to the following figure:

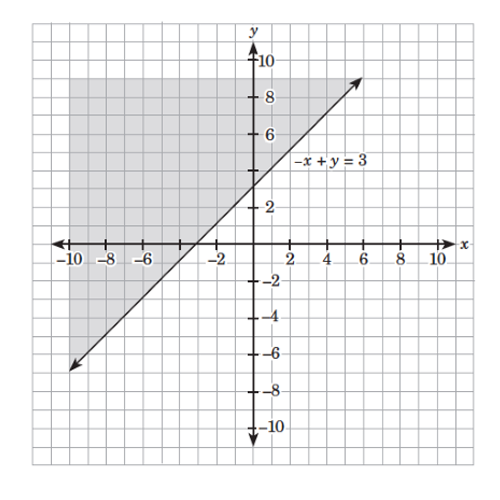
For $-x+y\ge 3,$ the boundary line is a solid line with the equation $-x+y=3.$ Using $(0,0)$ again as the test point, you will obtain $0\ge 3,$ which is false. Thus, the graph of $-x+y\ge 3$ is the region that does not contain the point $(0,0)$ and includes the boundary line, as shown in the following figure:

Combine the two preceding graphs on the same set of axes and shade the region where they overlap. The resulting region (which is shown in the figure below) is the solution set of the given system of linear inequalities.