Loading...
Linear Functions
A
B
C
. . . .

Basic Concepts on Linear Functions

In chapter 3, you have learned how to graph an equation in the form Ax+By+C=0, where A, B, and C are real numbers, and where both A and B are not equal to zero. Recall that its graph is a line, which may be horizontal, vertical, or neither. Any line other than a vertical line can represent the graph of a function. Such a function is called a linear function.

Example 1

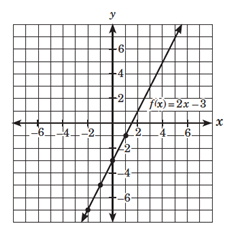
Given the linear function  f defined by f(x)=2x−3, determine its slope and y-intercept. Graph the given function.



Solution

The given function   f(x)=2x−3 is in the form   f(x)=mx+b. Thus, it is a linear function with slope m=2 and y-intercept b=−3. A slope of 2 means that there is a 2-unit increase in y for every unit increase in x. A y-intercept of –3 means that the graph of the function intersects the y-axis at y=−3. Using the technique you learned on graphing functions, construct a table of ordered pairs for   f(x)=2x−3.

Value of
x 		Value of
f(x)=2x−3 		Ordered Pair
(x, y) or (x, f(x))
–2 f(−2)=−7 (−2, −7)
–1 f(−1)=5 (−1, −5)
0 f(0)=−3 (0, −3)
1 f(1)=−1 (1, −1)

The graph of the function is shown in the figure below.