Fundamental Principle of Counting
In choosing your breakfast, you have 4 choices for the sandwich (egg, bacon, ham, or tuna), 3 choices for beverage (milk, coffee, or juice), and 2 choices for fruit (watermelon or banana). Suppose you are only allowed to choose one sandwich, one beverage, and one fruit. How many different combinations of breakfast are possible? List all the elements.
The given experiment can be divided into three operations: choosing the sandwich, choosing the beverage, and choosing the fruit. The first operation gives 4 possible outcomes, the second gives 3, while the third gives 2. Thus, Hence, there are 24 elements in the sample space.
Recall how to make a tree diagram such as the one given below.
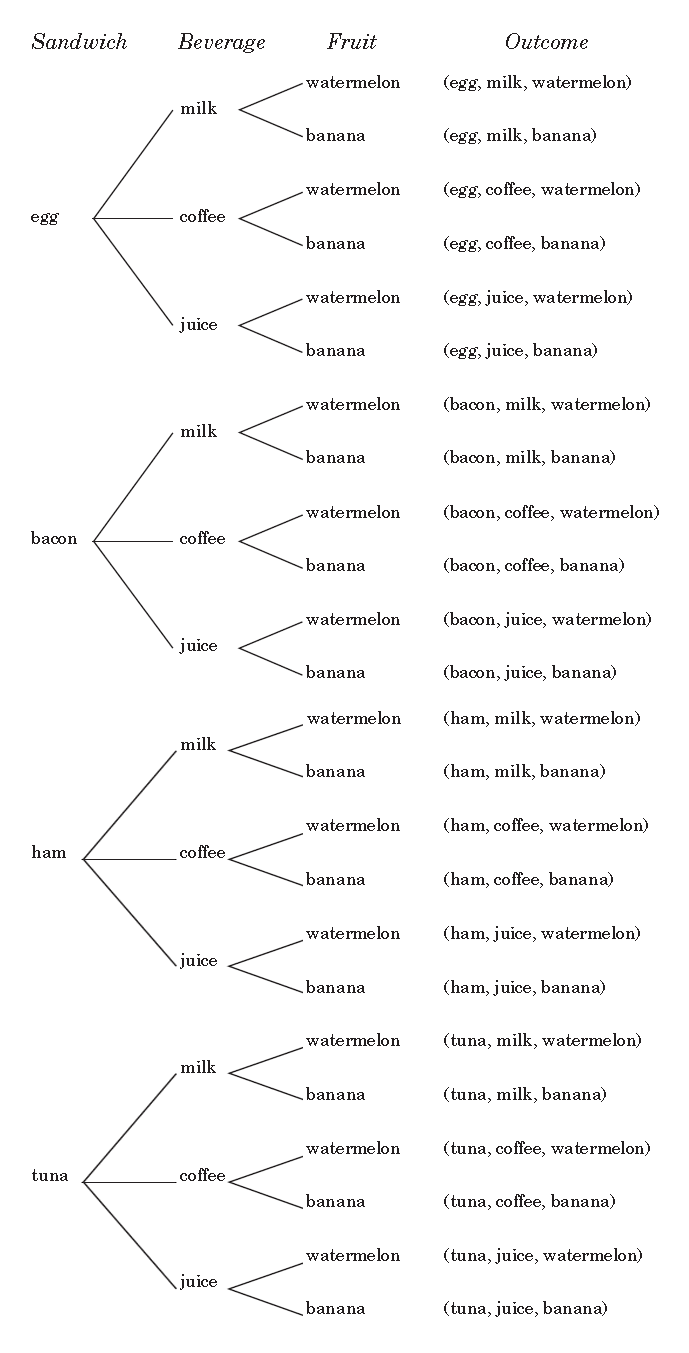
Therefore, the sample space S can be written as follows:
S = {(egg, milk, watermelon), (egg, milk, banana), (egg, coffee, watermelon), (egg, coffee, banana), (egg, juice, watermelon), (egg, juice, banana), (bacon, milk, watermelon), (bacon, milk, banana), (bacon, coffee, watermelon), (bacon, coffee, banana), (bacon, juice, watermelon), (bacon, juice, banana), (ham, milk, watermelon), (ham, milk, banana), (ham, coffee, watermelon), (ham, coffee, banana), (ham, juice, watermelon), (ham, juice, banana), (tuna, milk, watermelon), (tuna, milk, banana), (tuna, coffee, watermelon), (tuna, coffee, banana), (tuna, juice, watermelon), (tuna, juice, banana)}.
