EDGE Math 8

Triangle Inequalities

The converse of the Side-Angle Inequality Theorem is called Angle-Side Inequality Theorem.

Theorem. Angle-Side Inequality Theorem
If two angles of a triangle are not congruent, then the longer side lies opposite the larger angle.

Given:	$ΔABC$ with $m ∠ A > m ∠ C$
Prove:	$BC > AB$

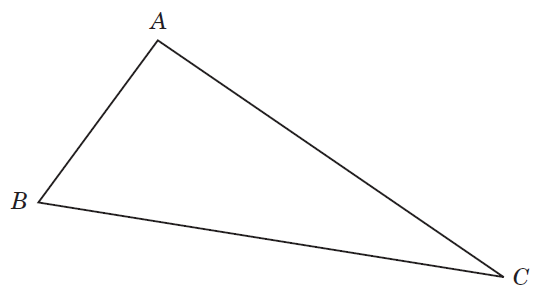
Proof:

There are three possibilities for the lengths BC and AB. These are the following:

BC < AB

BC = AB

BC > AB

If $BC < AB,$ then by the Side-Angle Inequality Theorem, $m ∠ A < m ∠ C .$ This is impossible since it contradicts the given condition that $m ∠ A > m ∠ C .$

If $BC = AB,$ then by the Isosceles Triangle Theorem, $∠ A ≅ ∠ C,$ which is false.

The only remaining possibility is $BC > AB .$ Therefore, if $m ∠ A > m ∠ C,$ then $BC > AB .$