EDGE Math 8

Example 1

An elevator in a mall has a capacity of 1350 kg. Suppose that on the average, a child weighs about 25 kg while an adult weighs 60 kg.

a.	Write a system of inequalities for the given situation. Then graph the solution set of the system.
b.	Is the ordered pair $(2, 10)$ a solution to the system? What information does the answer imply about the given problem?

Solution

a.	Let x = number of children and y = number of adults.

It is given that the sum of the weights of children and adults cannot exceed 1350 kg. This translates into

25 x + 60 y \leq 1350.

In addition, the number of children (x) and the number of adults (y) cannot be negative. Hence,

x \geq 0

and

y \geq 0.

You now have a system of inequalities.

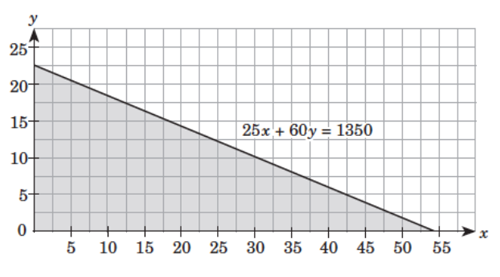
{\begin{array}{l} 25 x + 60 y \leq 1350 \\ x \geq 0 \\ y \geq 0 \end{array}

Graph each inequality of the system.
Graph of

25 x + 60 y \leq 1350 :

region on or below the line

25 x + 60 y = 1350

Graph of

x \geq 0

and

y \geq 0 :

first quadrant region together with the nonnegative sides of the x- and y-axes

The following figure shows the graph of the solution set of the system:

b.	To determine if $(2, 10)$ is a solution to the system, substitute 2 for x and 10 for y in the first inequality of the system.

\begin{array}{l} 25 (2) + 60 (10) \overset{?}{\leq} 1350 \\ 50 + 600 \overset{?}{\leq} 1350 \\ 650 \overset{?}{\leq} 1350 True \end{array}

Moreover, it is also true that

2 \geq 0

and

10 \geq 0.

Thus, the ordered pair

(2, 10)

is a solution to the system. This means that the combined weights of 2 children and 10 adults do not exceed the capacity of the elevator.