EDGE Math 8

Uniform Motion and Work Problems

The following examples involve word problems on uniform motion and work:

Example 1

Two buses leave the same station at the same time but travel in opposite directions. The first bus travels 15 km/h faster than the second bus. After 2 h, the buses are 270 km apart. Find the speed of the faster bus.

Solution

Represent the speeds of the two buses in kilometers per hour. Let x be the speed of the first bus and y be the speed of the second bus.

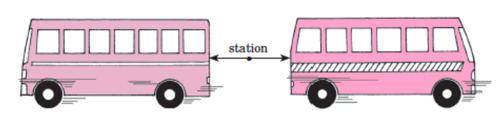
Use the formula $d = r t,$ where d is the distance traveled, r is the rate or speed, and t is the time.

Set up two equations based on the given conditions in the problem.

First equation: The speed of the first bus is 15 km/h more than the second bus, or

x = 15 + y .

Second equation: After 2 h, the distance traveled by the first bus plus the distance traveled by the second bus is equal to 270 km, or

2 x + 2 y = 270.

This results in the following system of equations:

{\begin{array}{l} x = 15 + y \\ 2 x + 2 y = 270 \end{array}

To solve the system of equations, substitute $15 + y$ for x in the second equation of the system.

$2 x + 2 y$	$= 270$
$2 (15 + y) + 2 y$	$= 270$
$(30 + 2 y) + 2 y$	$= 270$
$30 + 4 y$	$= 270$
$4 y$	$= 270 - 30$
$4 y$	$= 240$
$y$	$= \frac{240}{4}$
$y$	$= 60$

To solve for x, substitute 60 for y in $x = 15 + y;$ thus, you will have

x = 15 + 60 = 75.

Thus, the solution of the system is $(75, 60) .$

Checking

The speed of the first bus (which is 75 km/h) is 15 km/h more than the speed of the second bus (which is 60 km/h). Moreover, the total distance traveled by the buses in 2 h is

75 (2) + 60 (2) = 150 + 120 = 270 km .

The conditions of the problem are satisfied by the two numbers. Thus, the speed of the faster bus (or the first bus) is 75 km/h.