Functions

A relation is called a function if no two distinct ordered pairs in it have the same first coordinate. For example, the relation $\{(-1,3),(0,4),(1,4)\}$ is a function. On the other hand, the relation $\{(-1,3),(0,4),(-1,4)\}$ is not a function since the ordered pairs $(-1,3)$ and $(-1,4)$ have the same first coordinate, which is −1.

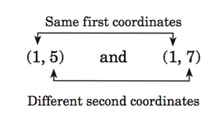
The set in the previous example,  $A=\{$$(1,120),(2,100),$$(3,180),(4,240)\}\text{,}$  is another example of a function. Note that each first coordinate is paired with exactly one second coordinate and that each second coordinate is also paired with exactly one first coordinate. This function is called a one-to-one function. A one-to-one function is a function in which no two different ordered pairs have the same second coordinate.