EDGE Math 8

Theorem. Only one line can be drawn through a point perpendicular to a given line.

Given:

Line l

Prove:

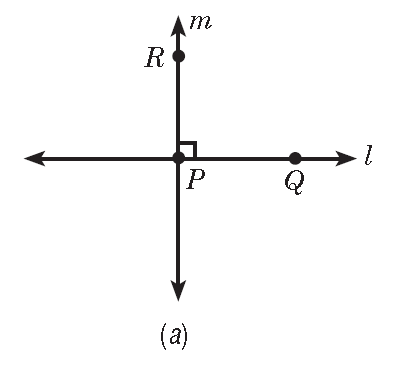
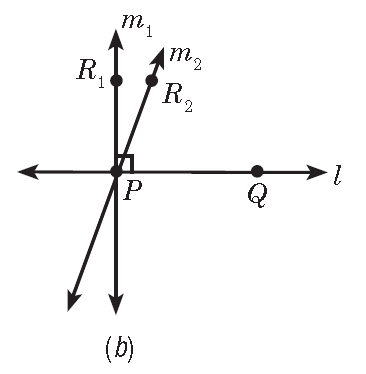
a.	There is a line m such that $m ⊥ l$ through point P.
b.	There is only one such line m.

Proof:

a.	Let point Q be any point on line l other than point P. There exists a $\overset{\leftrightarrow}{PR},$ with point R on the same plane as line l, such that $m ∠ R P Q = 90 °$ by the Angle Construction Postulate. Let line m be $\overset{\leftrightarrow}{PR} .$ Then $m ⊥ l$ at point P.

Suppose that there are two lines

m_{1}

and

m_{2}

perpendicular to line l at point P. Then line

m_{1}

contains

{\vec{PR}}_{1}

and

m_{2}

contains

{\vec{PR}}_{2},

with points

R_{1}

and

R_{2}

m_{1}

and

m_{2},

respectively. By the definition of perpendicular,

∠ R_{1} P Q

and

∠ R_{2} P Q

are right angles. By the Angle Construction Postulate,

{\vec{PR}}_{1}

and

{\vec{PR}}_{2}

must be the same ray. Hence,

m_{1}

and

m_{2}

cannot be different from each other, since these lines have more than one point in common. Therefore, line

m_{1}

is the same as line

m_{2} .