EDGE Math 8

Factoring Other Trinomials

Trinomials in the Form $a x^{2} + b x + c$

(Continuation from the previous slide)

Next, to get the last terms of the two binomial factors, you need to find two integers whose product is $- 15$ (which is the last term of the trinomial).

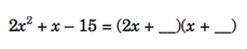
Since you are looking for integer factors of $- 15$ , the following are the possible last terms of the binomial factors:

- 15 = (- 15) (1)

- 15 = (15) (- 1)

- 15 = (- 3) (5)

- 15 = (3) (- 5)

Use these integer pairs to fill in the remaining blanks in the equation and to find the correct combination that will make the equation true. Thus, the following are the possible binomial factors:

(2 x - 1) (x + 15)

(2 x + 1) (x - 15)

(2 x - 3) (x + 5)

(2 x + 3) (x - 5)

(2 x - 15) (x + 1)

(2 x + 15) (x - 1)

(2 x + 5) (x - 3)

(2 x - 5) (x + 3)

Take a moment to study each pair of factors. Note that for each pair, the product of the first terms (the F in FOIL) is $2 x^{2}$ and the product of the last terms (the L in FOIL) is $- 15.$

(Continued in the next slide)